教育资讯：指数函数的性质

目前关于到指数函数的性质这一类的信息是很多小伙伴们都非常关心的，很多人也是经常在搜索关于指数函数的性质方面的信息，那么既然现在大家都想要知道此类的信息，小编就收集了一些相关的信息分享给大家。

指数函数的性质是：指数函数的定义域为R，这里的前提是a大于0且不等于1。对于a不大于0的情况，则必然使得函数的定义域不连续，因此我们不予考虑，同时a等于0函数无意义一般也不考虑。

基本性质

如图1所示为a的不同大小影响函数图形的情况

在函数中可以看到y=ax。

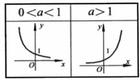
图1指数函数图像

（1）指数函数的定义域为R，这里的前提是a大于0且不等于1。对于a不大于0的情况，则必然使得函数的定义域不连续，因此我们不予考虑，同时a等于0函数无意义一般也不考虑。

（2）指数函数的值域为(0，+∞)。

（3）函数图形都是上凹的。

（4）a>1时，则指数函数单调递增；若0<a<1，则为单调递减的（图2）。

（5）可以看到一个显然的规律，就是当a从0趋向于无穷大的过程中（不等于0）函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置，趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递增函数的位置。其中水平直线y=1是从递减到递增的一个过渡位置。

图2指数函数增减性

（6）函数总是在某一个方向上无限趋向于X轴,并且永不相交。

（7）函数总是通过（0，1）这点,(若y=ax+b,则函数定过点(0,1+b))

（8）指数函数无界。

（9）指数函数是非奇非偶函数

（10）指数函数具有反函数，其反函数是对数函数，它是一个多值函数。

求解复杂指数类代数式的值时，需要注意以下几个方面

(1)当指数为负数时，一般先倒底，即先将底数变为倒数并将指数超威其相反数；

(2)当底数为小数时，一般将小数变为分数；

(3)对于根式，一般化为分数指数幂的形式；

(4)化简的最终结果要是最简形式，即不能既有根式又有分数指数幂的形式，也不能既有指数幂又有分母的形式，并且如果是二次根式，必须华为最简二次根式。

以上就是指数函数的性质这篇文章的一些介绍，网友如果对指数函数的性质有不同看法与以及，希望共同探讨进步。