原子光子相互作用的拓扑

自从发现量子霍尔效应以来，电子的拓扑相已成为凝聚态物理的一个主要研究领域。利用晶格位置之间的电子跳跃的特定工程，可以预测晶格中的许多拓扑阶段。不幸的是，天然晶格(晶体)中相邻位点之间的距离约为十亿分之一米，这使得这种工程非常困难。另一方面，光子晶体具有更大的规模。可见光的光子晶体的晶胞比电子大几千倍。因此，人们通过挖掘麦克斯韦方程和薛定inger方程之间的相似性而诉诸于拓扑相的光子模拟就不足为奇了，一个名为拓扑光子学的研究领域蓬勃发展。

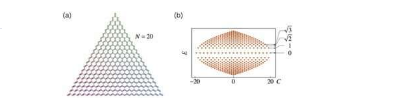
但是，光子和电子与狗和猫一样不同。光子本质上是社会性的。他们喜欢聚在一起(这就是为什么我们有激光)。电子彼此讨厌。根据费米排斥原则，他们有自己的领地。基于麦克斯韦方程和薛定inger方程之间的模拟的拓扑光子学属于经典光学，即电子波段拓扑的经典波模拟。很自然地要问，量化光是否嵌入了经典光学解释之外的新拓扑相位。最近，来自浙江大学的Han Han Cai和Wang Da-Wei揭示了量化光态晶格中的拓扑阶段。

光的能量只能存在于离散的包装中，一个非负整数加上hν的一半，其中h是普朗克常数，而v是光的频率。整数是该状态下的光子数，称为Fock状态，其中一半是由真空波动引起的。光能的这种离散性是解释黑体辐射光谱的关键(例如，在熔炉中，较高的温度会将光谱移至彩虹条的蓝色侧)。光量化也对原子光子产生深远影响互动。当光场中有n个光子时，被激发原子发射另一个光子的概率与n + 1成正比(请记住，光子是社会性的，他们喜欢新的成员加入)。当光被限制在空腔中时，原子发出的能量可以被重新吸收，这导致原子在激发态和基态之间振荡，并且振荡频率与n + 1的平方根成比例。当原子与光以Fock态叠加时耦合时，即在Jaynes-Cummings(JC)模型中，已观察到振荡频率的这些离散值的频谱，该模型已成为获取量子态的标准方法光。

JC模型与拓扑阶段无关，但能谱的整数平方根缩放使人联想到石墨烯中电子的Landau能级，该电子是拓扑阶段的摇篮。石墨烯中电子的能带在布里渊区边缘的两个点(称为狄拉克点)上接触，服从二维狄拉克方程的电子在其能量和动量之间具有线性关系。当施加磁场时，电子以离散频率进行回旋加速器运动，其离散频率与整数的平方根成比例，该整数对应于离散的Landau能级。蔡和王在磁场中建立了三模JC模型和狄拉克电子之间的联系。

　　免责声明：本文由用户上传，与本网站立场无关。财经信息仅供读者参考，并不构成投资建议。投资者据此操作，风险自担。 如有侵权请联系删除！